All Paths from Source Lead to Destination

Given theedgesof a directed graph, and two nodessourceanddestinationof this graph, determine whether or not all paths starting fromsourceeventually end atdestination, that is:

• At least one path exists from the

  source

  node to the

  destination

  node

• If a path exists from the

  source

  node to a node with no outgoing edges, then that node is equal to

  destination

  .

• The number of possible paths from

  source

  to

  destination

  is a finite number.

Returntrueif and only if all roads fromsourcelead todestination.

Example 1:

Input: 
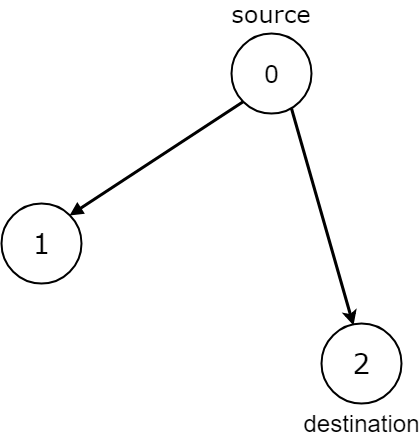
n = 3, edges = 
[[0,1],[0,2]]
, source = 
0
, destination = 2

Output: 
false
Explanation: 
It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

Input: 
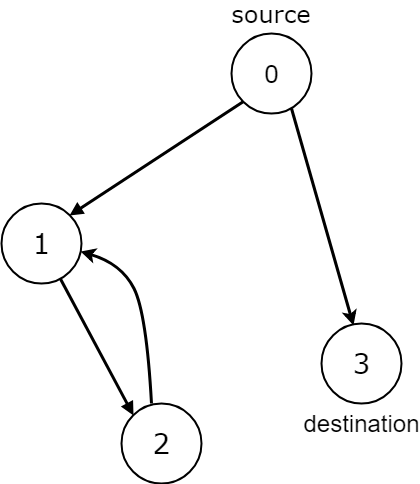
n = 
4
, edges = 
[[0,1],[0,3],[1,2],[2,1]]
, source = 
0
, destination = 
3
Output: 
false
Explanation: 
We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

Input: 
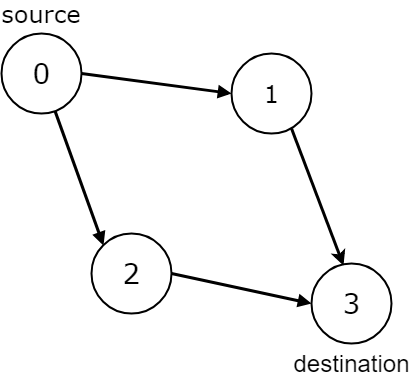
n = 
4
, edges = 
[[0,1],[0,2],[1,3],[2,3]]
, source = 
0
, destination = 
3
Output: 
true

Example 4:

Input: 
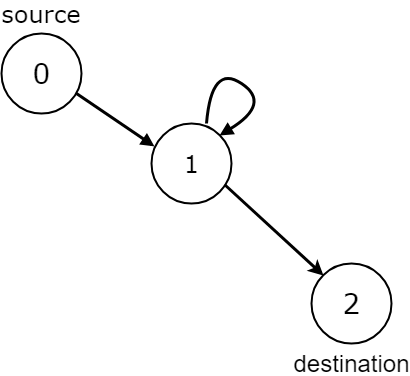
n = 
3
, edges = 
[[0,1],[1,1],[1,2]]
, source = 
0
, destination = 
2
Output: 
false
Explanation: 
All paths from the source node end at the destination node, but there are an infinite number of paths, such as 0-1-2, 0-1-1-2, 0-1-1-1-2, 0-1-1-1-1-2, and so on.

Example 5:

Input: 
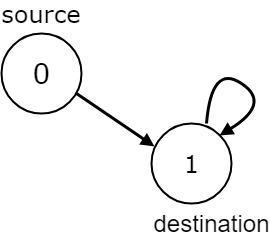
n = 
2
, edges = 
[[0,1],[1,1]]
, source = 
0
, destination = 
1
Output: 
false
Explanation: 
There is infinite self-loop at destination node.

Note:

The given graph may have self loops and parallel edges.
The number of nodes n in the graph is between 1 and 10000
The number of edges in the graph is between 0 and 10000
0 <= edges.length <= 10000
edges[i].length == 2
0 <= source <= n - 1
0 <= destination <= n - 1

分析

一条道带一个path(set), 在子dfs前加入，loop完了去掉。有回溯

不是起点也不是终点，返错，要不继续往下探索

class Solution:
    def leadsToDestination(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        g = {}
        for a,b in edges:
            g.setdefault(a,[]).append(b)
        if destination in g:
            return False

        def dfs(root,path):            
            if root not in g:
                return root == destination                

            path.add(root)
            for n in g[root]:
                if n in path or not dfs(n,path):
                    return False
            path.remove(root)   
            return True


        return dfs(source,set())


        。