Binary Search Tree to Greater Sum Tree

Given the root of a binary search tree with distinct values, modify it so that every node has a new value equal to the sum of the values of the original tree that are greater than or equal to node.val.

As a reminder, a binary search tree is a tree that satisfies these constraints:

• The left subtree of a node contains only nodes with keys less than the node's key.

• The right subtree of a node contains only nodes with keys greater than the node's key.

• Both the left and right subtrees must also be binary search trees.

Example 1:

Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

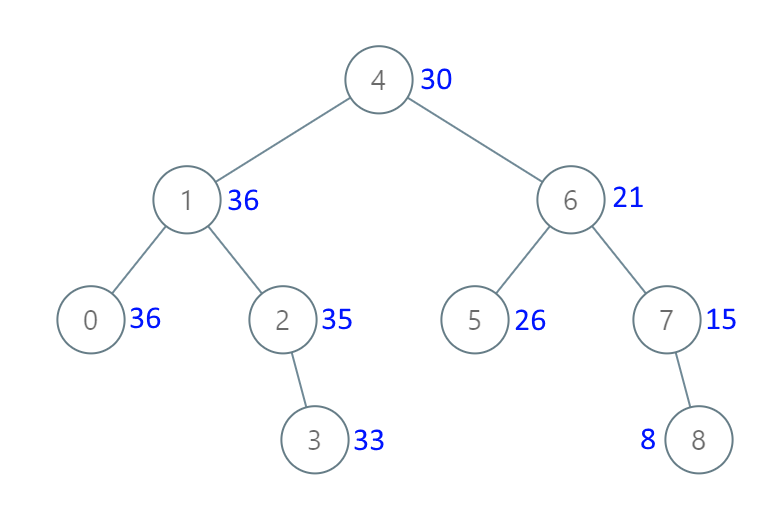
Note:

1. The number of nodes in the tree is between 1and 100.

2. Each node will have value between 0 and 100.

3. The given tree is a binary search tree.

分析

就是右中左，然后替换val为current sum

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    val=0
    def bstToGst(self, root: TreeNode) -> TreeNode:
#         self.sm = 0
#         def helper(root):
#             if not root:
#                 return self.sm
            
#             helper(root.right)
#             self.sm += root.val
#             root.val = self.sm
#             helper(root.left)
            
#         helper(root)
#         return root
        if root.right: self.bstToGst(root.right)
        root.val = self.val = self.val + root.val
        if root.left: self.bstToGst(root.left)
        return root
        
            
        
        

不懂为什么返回左子树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        def helper(root,sm):
            if not root:
                return sm
            root.val += helper(root.right,sm)
            return helper(root.left,root.val)
        helper(root,0)
        return root
        

Recursive

这里stack装的是右子树，记得开始是把root塞进去stack

这里需要全局变量sum来记录当前的sum

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        stack = []
        cur = root
        sm = 0
        while stack or cur:
            while cur:
                stack.append(cur)
                cur = cur.right
            cur = stack.pop()
            cur.val += sm
            sm = cur.val
            cur = cur.left
        return root