N-Queens

Then-queens puzzle is the problem of placingnqueens on ann×nchessboard such that no two queens attack each other.

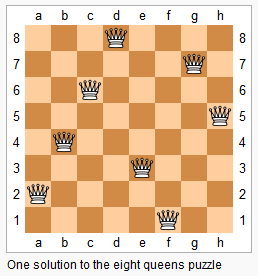
Given an integern, return all distinct solutions to then-queens puzzle.

Each solution contains a distinct board configuration of then-queens' placement, where'Q'and'.'both indicate a queen and an empty space respectively.

For example, There exist two distinct solutions to the 4-queens puzzle:

[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

分析

结论

图形	适用公式	说明
正方形	abs(Δrow) == abs(Δcol)	对角线行差和列差绝对值相等
长方形	Δrow / Δcol == ±(height/width)	需按长宽比例判断

这是一个回溯法解决N皇后问题的代码。

• 棋盘表示：用 List<String> 表示一个棋盘，每个 String 是一行的布局（如 "Q... 表示皇后在第1列）。

• 核心思路：

  1. 用 cols 记录每行皇后的列位置（如 [1,3,0,2] 表示第0行放第1列，第1行放第3列等）。

  2. DFS逐行放置：每层递归处理一行，尝试所有可能的列位置，通过 isValid 检查是否冲突（列、对角线）。

  3. 终止条件：当 row 填满（cols.size() == n），生成棋盘并加入结果。

关键点：

• cols 直接存储每行皇后的列下标（如 [2,0,3,1]），而非二维数组。

• 验证冲突：只需检查当前列是否已被占用，或与之前皇后是否在同一对角线（|row1 - row2| == |col1 - col2|）。

• 效率：通过回溯剪枝，避免无效尝试。

示例：

对于4皇后问题，一个合法解 cols = [1,3,0,2] 对应的棋盘：

.Q..  
...Q  
Q...  
..Q.  

cols.get(i) ==col
判断是否在斜线上，看row和col差或者合是否相等，loop此时cols所有行。row = cols.size()，col是此时dfs的试探点。
i - cols.get(i) == row - col 左上到右下
i + cols.get(i) ==row + col 右上到左下

该公式仅在 正方形的对角线（即行差和列差的绝对值相等）时成立。对于长方形，对角线不一定满足 |Δrow| == |Δcol|
虽然直接比较差/和更直观，但绝对值公式：
abs(row1 - row2) == abs(col1 - col2)
实际上是数学等价的，因为它同时覆盖了：
主对角线（row-col相等 → 行差等于列差）
副对角线（row+col相等 → 行差等于负的列差 → 绝对值相等）

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> ret = new ArrayList<>();
        if(n < 1){
            return ret;
        }        
        List<Integer> cols = new ArrayList<Integer>();       
        dfs(n, cols, ret);  
        return ret;
    }

    List<String> draw(int n, List<Integer> cols){
        List<String> ret = new ArrayList<String>();       
        for(int i = 0; i < n ; i ++){
            StringBuilder sb = new StringBuilder();
                for(int j = 0; j < n ; j ++){
                    sb.append(cols.get(i) == j ? "Q" : ".");
                }
                ret.add(sb.toString());
            }  
        return ret;
    }

    void dfs(int n, List<Integer> cols, List<List<String>> ret){
        if(cols.size() == n){
             ret.add(draw(n, cols));    
            return;
        }
        for(int i = 0; i < n ; i ++){
        //i就是当前col的位置          
        if(isValid(i,cols)){
                cols.add(i);
                dfs(n, cols, ret);
                cols.remove(cols.size() - 1);
            }
        }
    }

    boolean isValid(int col, List<Integer> cols){
        int row = cols.size();
        for(int i = 0; i < row;  i ++){
           if(cols.get(i) == col || cols.get(i) - i == col - row || cols.get(i) + i == col + row) {
               return false;
           }            
        }
        return true;
    }
}