1235. Maximum Profit in Job Scheduling

interval,二分

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

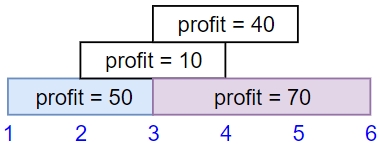
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

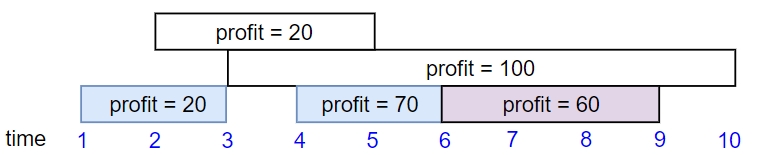
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 104

• 1 <= startTime[i] < endTime[i] <= 109

• 1 <= profit[i] <= 104

分析：主要是bisect.bisect_right的用法，返回index 需要-1。

1. Sorting: We first sort all jobs by their end time to enable efficient binary search for compatible jobs.

2. Dynamic Programming Array:

   • dp[i] stores the maximum profit achievable with the first i jobs

   • We initialize dp[0] = 0 (base case: no jobs = no profit)

3. Processing Each Job:

   • For each job, we find the last job that doesn't overlap with it using binary search

   • We then compare:

     • Taking the current job plus the profit from the last compatible job

     • Not taking the current job (keeping the previous maximum)

   • We store the maximum of these two options in dp[i]

4. Result: The final answer is in dp[n], representing the maximum profit from all jobs.

```python3

class Solution:
    def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
        jobs = sorted(zip(startTime, endTime, profit), key=lambda x: x[1])
        n = len(jobs)
        dp = [0]*(n+1)
        ends = [e for s,e,f in jobs]
        for i in range(1,n+1):
            s, e, p = jobs[i-1]
            j = bisect.bisect_right(ends, s) - 1
            if j >= 0:
                dp[i] = max(dp[i-1], dp[j+1] + p)
            else:
                dp[i] = max(dp[i-1], p)
        return dp[n]
```