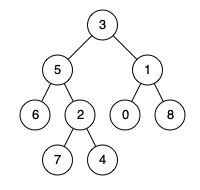
1650. Lowest Common Ancestor of a Binary Tree III

双指针相遇类

Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).

Each node will have a reference to its parent node. The definition for Node is below:

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

According to the definition of LCA on Wikipedia: "The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)."

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

• The number of nodes in the tree is in the range [2, 105].

• -109 <= Node.val <= 109

• All Node.val are unique.

• p != q

• p and q exist in the tree.

分析：

数学本质：

• 所有相遇问题都可转化为追及问题

• 通过设定不同的步长比（如1:2, m:n）解决不同场景

是否树形结构？
├─ 是 → 是否有parent指针？
│   ├─ 是 → 使用LCA双指针法（本题）
│   └─ 否 → 需要递归查找
└─ 否 → 是否为环形检测？
    ├─ 是 → 快慢指针法
    └─ 否 → 相向指针/滑动窗口

对比 另一个LCA 提供ROOT 自顶向下，parent指针提供反向移动能力

1. 总步数相同

   • 第一次遍历：

     • pointer1 走 a 步到 LCA，再走 b 步到 q 的起始位置。

     • pointer2 走 b 步到 LCA，再走 a 步到 p 的起始位置。

     • 这里省略到LCA到ROOT距离，因为这一段是重复的。双方都走可抵消。

   • 第二次遍历：

     • 此时，pointer1 和 pointer2 都走了 a + b 步，必定在 LCA 处相遇。

   有点类似快慢指针的思想

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""

class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        a,b = p,q
        while a != b:
            a = a.parent if a else q
            b = b.parent if b else p
        return a